Problem współliniowość

Jak zmierzyć wpływ poszczególnych atrybutów, na zmienną endogeniczną? Podstawową techniką do pomiaru wpływu zmiennych objaśniających (atrybuty) na zmienną objaśnianą (zmienna celu) będzie oszacowanie prostego modelu ekonometrycznego. W przypadku, gdy zmienna celu jest zmienną ciągłą (np. poziom zarobków poszczególnych osób, cena nieruchomości, poziom ciśnienia tętniczego), poprzez prosty model możemy rozumieć model regresji liniowej. W przypadku gdy zmienna celu jest zmienną dyskretną – np. zmienną binarną – poprzez prosty model rozumieć będziemy model regresji logistycznej$^1$.

Po etapie szacowania modelu można przejść etapu analizy wartości parametrów takiego modelu – w przypadku tych prostych modeli, można wprost analizować parametry $\beta_i, \forall_i$ modelu. Im wyższa wartość parametru $\beta_i$, tym większy wpływ zmiennej objaśniającej na zmienną objaśnianą.

Problem z analizą wpływu poszczególnych atrybutów, tak zaproponowaną, związany jednak jest z przyjęciem (często milcząco) założenia, że atrybuty modeli nie są ze sobą skorelowane.

Materiał/dane, z którym ekonometria często pracuje nie pochodzi z kontrolowanego przez badacza doświadczenia/środowiska$^2$ – dane pochodzą z “prawdziwego” życia, a żaden polityk nie zmieni poziomu stóp procentowych, żeby zweryfikować ich wpływ na poziom bezrobocia$^3$. Przekłada się to na często problemy z danymi, takie jak: występujące braki wartości atrybutów, zbyt mało obserwacji, nadmierne zagregowanie danych, lub występowanie nadmiernej korelacji między zmiennymi objaśniającymi.

Współliniowość – o niej dziś jest mowa – to wada próby statystycznej, związana z występowaniem “nadmiernej” korelacji między atrybutami. Występowanie tej korelacji, a w efekcie współliniowości (ang. multicollinearity), wpływa na możliwość pomiaru wpływu poszczególnych atrybutów na zmienną endogeniczną. Jest to cecha zbioru danych, na którym wykonywana jest analiza, która występuje zawsze na rzeczywistych danych – jedynie zmienne sztuczne mogą charakteryzować się pełną niezależnością$^2$.

Dzisiejszy post bazuje w dużej mierze na książce Ekonometria, autorstwa prof. Aleksandra Welfe, wydanie 1995.

Prosty przykład symulacyjny

Przyjmijmy$^4$, że znamy proces generujący dane (ang. underlying process); proces ten zakłada, że na zmienną celu $y$ wpływają dwie zmienne egzogeniczne $X_1$ i $X_2$:

$y = 0.5X_1 + 0.3X_2 + \xi$

Niech $\xi \sim N(0,1)$, a zmienne $X_1$ i $X_2$ pochodzą z rozkładu łącznego $(X_1, X_2) \sim N(0, \Sigma)$, gdzie:

\begin{equation} \Sigma = \sigma R \sigma = \begin{bmatrix} \sigma_{X_1} & 0 \\ 0 & \sigma_{X_2} \end{bmatrix} \begin{bmatrix} 1 & \rho \\ \rho & 1 \end{bmatrix} \begin{bmatrix} \sigma_{X_1} & 0 \\ 0 & \sigma_{X_2} \end{bmatrix} \end{equation}

Niech $\sigma_{X_1} = 1$, oraz $\sigma_{X_2} = 2$

Poniżej zaprezentowano symulację powyższego scenariusza, z uwzględnieniem estymacji modelu $\hat{y} = \beta_1 X_1 + \beta_2 X_2$. Na początek importujemy wszystkie potrzebne biblioteki

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression

Następnie definiujemy główne zmienne wykorzystywane w symulacji:

N = 500 #Number of observations
X_VAR = np.array([1.0, 4.0], dtype = np.float64)
BETAS = np.array([0.5, 0.3], dtype = np.float64)

Następnie losujemy wartości atrybutów oraz błędów modelu:

np.random.seed(111)
x_base = np.random.randn(N, 2) * np.sqrt(X_VAR) #Base of attributes
x_comm = np.repeat(np.random.randn(N, 1), 2, axis = 1) * np.sqrt(X_VAR) #Common factor for attributes
y_eps  = np.random.randn(N, 1) #Epsilon for random factor

Mając definicję atrybutów x oraz błędów modelu y_eps możemy dokonać estymacji modelu regresji liniowej, dla różnych wartości korelacji między zmiennymi $X_1$ i $X_2$:

results = {}; k = 0
for i in np.linspace(0, 0.99, 10000):
    #Create X and y
    x = x_base * (1 - i) + x_comm * i
    y = np.sum(BETAS * x, axis = 1).reshape(-1, 1) + y_eps
    
    #Model estimation
    reg   = LinearRegression(fit_intercept=True).fit(x, y)
    y_hat = reg.predict(x)
    
    #Calculate model performance
    r_2 = 1 - np.sum((y_hat - y)**2) / np.sum((y - np.mean(y))**2)
    mse = sum((y-y_hat)**2)/(N-2)
    
    #Calculate estimator values 
    x_corr = np.corrcoef(x[:,0], x[:,1])[0][1]
    b1 = reg.coef_[0][0]
    b2 = reg.coef_[0][1]
    b_V =  mse * np.linalg.inv(np.transpose(x).dot(x)).diagonal() # MSE * (X^T*X)^1
    b1_v = np.sqrt(b_V[0])
    b2_v = np.sqrt(b_V[1])
    
    #Append results
    results[k] = {"r_2" : r_2, "corr": x_corr,  
                  "b1": b1, "b2": b2,
                  "b1_v": b1_v, "b2_v": b2_v}; k += 1
    
results = pd.DataFrame.from_dict(results, orient = "index")

Mając zagregowane wartości wyników z modelu przygotujmy wykresy wartości i odchyleń standardowych parametrów dla różnych wartości korelacji między poszczególnymi zmiennymi objaśniającymi.

# Define figure
fig = plt.figure(figsize=(9, 4))
fig.subplots_adjust(wspace=0.3, hspace=0.3)

# Define x-values
index = np.linspace(0, 0.99, 10000)

# Plot AXIS 1: model coefficients
ax1 = plt.subplot(121)
ax1.plot(index, np.interp(index, results['corr'].values, results['b1'].values),
         label = '$X_1$', color = 'black', linestyle = '-')
ax1.plot(index, np.interp(index, results['corr'].values, results['b2'].values),
         label = '$X_2$', color = 'black', linestyle = '-.')
ax1.set_title('Wartość oszacowanych \n parametrów')
ax1.set_xlabel('Współczynnik korelacji')
ax1.set_xlim([0, 1]), ax1.set_ylim([-1, 1])

# Plot AXIS 2: Coefficients' standards deviations
ax2 = plt.subplot(122)
ax2.plot(index, np.interp(index, results['corr'].values, results['b1_v'].values),
         label = '$\\beta_1$', color = 'black', linestyle = '-')
ax2.plot(index, np.interp(index, results['corr'].values, results['b2_v'].values),
         label = '$\\beta_2$', color = 'black', linestyle = '-.')
ax2.set_title('Odchylenie standardowe \n wartości parametrów')
ax2.set_xlabel('Współczynnik korelacji')
ax2.set_xlim([0, 1]), ax2.set_ylim([0, 1])

# Legend
handles, labels = ax2.get_legend_handles_labels()
fig.legend(handles, labels, loc='lower center', ncol=3)
plt.subplots_adjust(bottom=0.2)

plt.show()

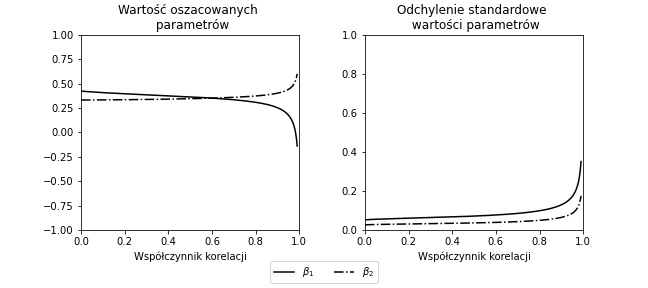
drawing

Wnioski:

Dla niskiej wartości korelacji oszacowane parametry modelu są zbliżone do tych, które założyliśmy w procesie generowania danych (choć występuje przesunięcie dla zmiennej $\beta_1$ w procesie bazowym wynosi $0.5$).
Wraz ze wzrostem korelacji między zmiennymi $X_1$ i $X_2$ powoduje zmianę wartości szacowanego parametru; zmiana wartości szacowanego parametru jest większa dla zmiennej o mniejszej wariancji.
Zmiana wartości szacowanego parametru może być na tyle istotna, że zmienia się znak tego parametru (patrz $\beta_1$ dla dużej wartości korelacji).
Oszacowany parameter dla zmiennej o większej wariancji (tj. $\sigma_{X_1} = 1 < \sigma_{X_2} = 2$) ma mniejszą wariancję (patrz wariancja parametru $\beta_1$ jest większa niż wariancja parametru $\beta_2$).

Analogiczny eksperyment przeprowadzono dla większej liczby obserwacji N = 5.000 – przypadek, w którym estymacja parametrów odbywa się na większej próbie:
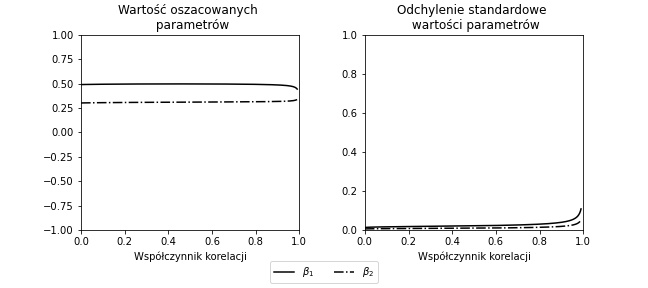
drawing

Podsumowanie przykładu symulacyjnego

Dla dużych wartości korelacji między zmiennymi oszacowane parametry między zmiennymi mogą istotnie zmieniać wartość, a nawet znak. Fakt ten wynika z wariancji estymatorów – przy wyższym poziomie korelacji między zmiennymi objaśniającymi, wariancja estymatorów również rośnie.

Oznacza to, że interpretacja oszacowanych parametrów modelu, bez równoczesnego uwzględnienia wartości korelacji między korespondującymi atrybutami może prowadzić do niepoprawnych wniosków. Jednym z prostych rozwiązań problemu współliniowości może być zwiększenie liczności próby na jakiej szacowany był model (parametr N).

Źródło współliniowości

Tak jak wspomniano wcześniej, współliniowość jest wadą próby statystycznej$^2$. Jako źródła współliniowości można wskazać$^4$:

błędna specyfikacja modelu, np. transformując zmienne do formatu dummy variable (enkodowanie zmiennych ciągłych lub kategorycznych do formatu binarnego), włączenie wszystkich utworzonych zmiennych binarnych do modelu (również zmiennej referencyjnej).
dane wejściowe, tj. wykorzystanie w modelu ekonometrycznym wysoce skorelowanych zmiennych objaśniających

Z powyższymi źródłami związane są dwa typy współliniowości: doskonała i przybliżona współliniowość.

Współliniowość doskonała

Załóżmy następujący przykład modelu konsumpcji$^3$:

$C_t = \alpha_0 + \alpha_1 Y_t + \alpha_2 W_t + \alpha_3 N_t + \xi_t$

gdzie: $C_t$ to poziom konsumpcji, $Y_t$ to dochód, $W_t$ to dochód z pracy, $N_t$ to dochody pozostałe. Oznacza to, że:

$Y_t = W_t + N_t$

Zwróćmy uwagę, że przedstawiony model konsumpcji zawiera zmienną $Y_t$, która jest kombinacją liniową zmiennych $W_t$ oraz $N_t$. Dodatkowo, należałoby empirycznie zweryfikować, czy dochód z pracy $W_t$ nie jest skorelowany z dochodem pozostałym $N_t$.

Pomnóżmy teraz algebraicznie obie strony równości przez dowolną stałą $a\in \mathbb{R}$:

$0=aY_t-aW_t-aN_t$

Zestawiając powyższe z modelem konsumpcji uzyskujemy:

$C_t = \alpha_0 + (\alpha_1+a) Y_t + (\alpha_2-a) W_t + (\alpha_3-a) N_t + \xi_t$

Wartość oczekiwana $E[C]$ dla obu wskazanych równań na $C_t$ ma identyczną wartość (zwróć uwagę, że $\alpha_0$, $\alpha_1$, $\dots$ pozostaje niezmieniona). Oznacza to, że można do parametrów oszacowanego modelu dodać dowolną stałą $a$, a równanie dalej “będzie działać”. Wskazane zagadnienie estymacji jest zatem nieoznaczone (tj. jest spełnione dla nieskończonej liczby zbiorów wartości $\alpha_0$, $\alpha_1$, $\alpha_2$ i $\alpha_3$ przy założeniu różnych wartości zmiennej $a$).

Współliniowość przybliżona

Wcześniej wskazany przykład przedstawia sytuację, w której z perspektywy “technicznej” pracowaliśmy przy źle wyspecyfikowanym modelu – modelu, w którym rząd macierzy zmiennych objaśnianych $X$ nie był pełen (zmienna $Y_t$ była kombinacją liniową zmiennej $W_t$ oraz $N_t$).

Innym zagadnieniem, niezwiązanym ze złą specyfikacją modelu, jest występowanie tzw. współliniowości przybliżonej.

Bardzo dobrą pozycją referencyjną uzupełniającą wcześniejsze jest artykuł A caution regarding rules of thumb for variance inflation factors$^5$.

Wpłwy przybliżonej współliniowości (przedstawionej również we wcześniejszym przykładzie symulacyjny) jest dobrze obrazowany przez następujące równanie$^5$:

$\hat{\sigma}^2(\beta_i) = \frac{1}{n-k-1} \frac{1-R^2_y}{1-R^2_i} \frac{\Sigma_{j=1}^n (Y_j-\bar{Y})^2}{\Sigma_{j=1}^n (X_{i,j}-\bar{X_{i,.}})^2}$

gdzie: $n$ oznacza liczbę obserwacji, $k$ oznacza liczbę zmiennych w wykorzystanych modelu, $R^2_y$ oznacza współczynnik determinacji modelu, $R^2_i$ oznacza współczynnik determinacji modelu, w którym zmiennymi objaśniającymi są wszystkie zmienne objaśniające poza zmienną $X_i$, a zmienną objaśnianą jest zmienna $X_i$

Wariancja parametru $\beta_i$ zależy zatem od:

wielkości zbioru treningowego $n$–czym większy zbiór treningowy, tym mniejsza wariancja parametru $\beta_i$.
liczby zmiennych w modelu $k$–czym większa liczba zmiennych, tym większa wariancja parametru $\beta_i$.
jakości prognostycznej wszystkich zmiennych modelu $R^2_y$–im wyższa moc prognostyczna zmiennych $X_j$, $\forall_j$, tym mniejsza wartość wariancji parametru $\beta_i$. Oznacza to, że sumarycznie im lepszy model jest oszacowany, tym mniejszą wariancję średnio wszystkie parametry zmiennych powinny posiadać.
wielkości korelacji/zależności liniowej między pozostałymi zmiennymi a zmienną $X_i$–czym większa część wariancji zmiennej $X_i$ tłumaczonej przez pozostałe zmienne, tym większa wariancja parametru $\beta_i$.
zmienności zmiennej objaśnianej $\Sigma_{j=1}^n (Y_j-\bar{Y})^2$–czym większa zmienność zmiennej $Y$ tym większa wariancja parametru $\beta_i$.
zmienności zmiennej objaśniającej $\Sigma_{j=1}^n (X_{i,j}-\bar{X_{i,.}})^2$–czym większa zmienność zmiennej $X_i$ tym mniejsza wariancja parametru $\beta_i$.

Pomiar współliniowości

Do pomiaru zjawiska współliniowości występującego w modelach ekonometrycznych można wykorzystać jedno z dwóch narzędzi:
Indeks Warunkowy - ang. Condition Index

$CI_k = \frac{\lambda_{max}}{\lambda_{k}}^\frac{1}{2}$

gdzie $\lambda_{k}$ to $k$-ta wartość własna wyznaczona ze znormalizowanej macierzy atrybutów $X$. Wartością progową dla Indeksów Warunkowych jest wartość $15$–warto jednak zaznaczyć, że tzw. rule of thumb jest niejednoznaczna i powinna być postrzegana przez pryzmat konkretnego, analizowanego przypadku (więcej o tym w O’brien 2007).

Czynnik Inflacji Wariancji - ang. Variance Inflation Factor

$VIF_i = \frac{1}{1-R^2_i}$

gdzie: $R^2_i$ oznacza współczynnik determinacji modelu, w którym zmiennymi objaśniającymi są wszystkie zmienne objaśniające poza zmienną $X_i$, a zmienną objaśnianą jest zmienna $X_i$ Wartością progową dla Czynników Inflacji Wariancji jest między $5$ a $10$–analogicznie jak wcześniej, należy zawsze oceniać wartości parametrów VIF z perspektywy poszczególnych przypadków.

Główną różnicą między wskazanymi podejściami do pomiaru współliniowości jest to, że Indeks Warunkowy wyznaczany jest na poziomie wszystkich zmiennych objaśniających, a Czynniki Inflacji Wariacji na poziomie pojedynczej zmiennej.

Metody radzenia sobie ze współliniowością

Literatura$^2$ wskazuje na kilka możliwych strategii radzenia sobie z problemem przybliżonej współliniwości:

Brak akcji–w przypadku gdy współliniowość jest stosunkowo niewielka (np. wskazane wartości progowe miar współliniowości nie są przekroczone, a zmienne są statystycznie istotne).
Zmiana zakresu próby statystycznej–wybranie innego zakresu zbioru treningowego, może obniżyć problem współliniowości, np. gdy pierwsze obserwacje charakteryzują się niską wariancją–początki procesu zbierania danych mogą być “trudne” ;)
Wykorzystanie metod regularyzacji–nałożenie restrykcji na zmienne objaśniające (Lasso, Ridge Regression, Elastic Net, CART tree-pruning), lub redukcja wymiaru zmiennych objaśniających (PCA).
Transformacje na zmiennych–przeprowadzenie transformacji na zmiennych zwiększających ich wariancję, np. pierwsze różnice, logarytmowanie.
Usunięcie zmiennych objaśniajacych z modelu–należy pamiętać, że w przypadku gdy usuwana zmienne jest zmienną statystycznie istotną, powstały model będzie charakteryzować się obciążonością–Problem pominiętej zmiennej.

$^1$W przypadku gdy mamy problem wieloklasowy, zamiast pojedynczej regresji logistycznej, można przeprowadzić regresję logistyczną dla każdej z klas – takie podejście jest nazywane Multinomial logistic regression
$^2$Welfe, A. (1995). Ekonometria: metody i ich zastosowanie. Państwowe Wydaw. Ekonomiczne.
$^3$W krótkim horyzoncie faktycznie zależność taka powinna występować (walka z inflacją – podnoszenie stóp procentowych – powinna powodować pojawianie się bezrobocia); w długim horyzoncie czasu taka zależność nie występuje Phillips curve
$^4$Kaszyński, D., Kamiński, B., Szapiro, T., (2021). Credit Scoring in Context of Interpretable Machine Learning. Warsaw School of Economics
$^5$O’brien, R. M. (2007). A caution regarding rules of thumb for variance inflation factors. Quality & quantity, 41(5), 673-690.